

In the previous chapter we looked only at nonhomogeneous differential equations in which g(t) g ( t) was a fairly simple continuous function. Therefore the inverse Laplace transform gives $t^p$, as it should. The Laplace integral or the direct Laplace transform of a function f(t) defined for 0 t < is the ordinary calculus integration problem. Laplace transform In mathematics, the Laplace transform, named after its discoverer Pierre-Simon Laplace ( / lpls / ), is an integral transform that converts a function of a real variable (usually, in the time domain) to a function of a complex variable (in the complex frequency domain, also known as s-domain, or s-plane ). Laplace transforms comes into its own when the forcing function in the differential equation starts getting more complicated. The Laplace transformation converts a function in. We can then change variables immediately to get the $t$-dependence out of the way: if $z=st$, the integral becomes s 29-37 ODEs AND SYSTEMS LAPLACE TRANSFORMS Find the transform, indicating the method used and showing Solve by the Laplace transform, showing the details and graphing the solution: 29. They are perhaps one of the most useful transforms, second only to the famed Fourier transforms in utility. (If $t \leq 0$, we can keep pushing the contour to the right and make the integral as small as we like, so the inverse transform gives $0$ there as it should).
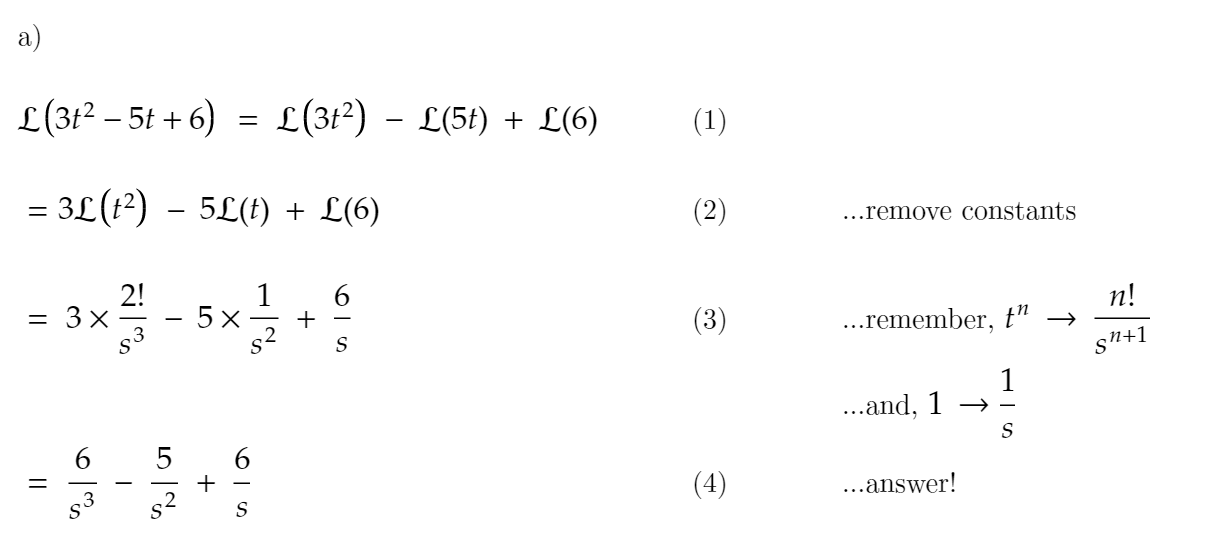
These can be used to solve differential equations and to convert from the time domain to s. The Laplace transform is a mathematical tool which converts the differential equations in time domain into algebraic equations in the frequency domain (or s-domain).Suppose $t>0$. This table lists some of the important Laplace Transforms. F(s) is always the result of a Laplace transform and f(t) is always the result of an Inverse Laplace transform, and so, a general table is actually a table of. Recall the definition of hyperbolic functions. s 29-37 ODEs AND SYSTEMS LAPLACE TRANSFORMS Find the transform, indicating the method used and showing Solve by the Laplace transform, showing the details and graphing the solution: 29.
#Laplace transform chart series#
I generally spend a couple of days giving a rough overview of the omitted chapters: series solutions (Chapter 4) and difference equations (Chapter 7). Table of Laplace Transforms Table Notes This list is not a complete listing of Laplace transforms and only contains some of the more commonly used Laplace transforms and formulas.

The linear time invariant (LTI) system is described by differential equations. first- and second-order equations, followed by Chapter 5 (the Laplace transform), Chapter 6 (systems), Chapter 8 (nonlinear equations), and part of Chapter 9 (partial differential equations).


 0 kommentar(er)
0 kommentar(er)
